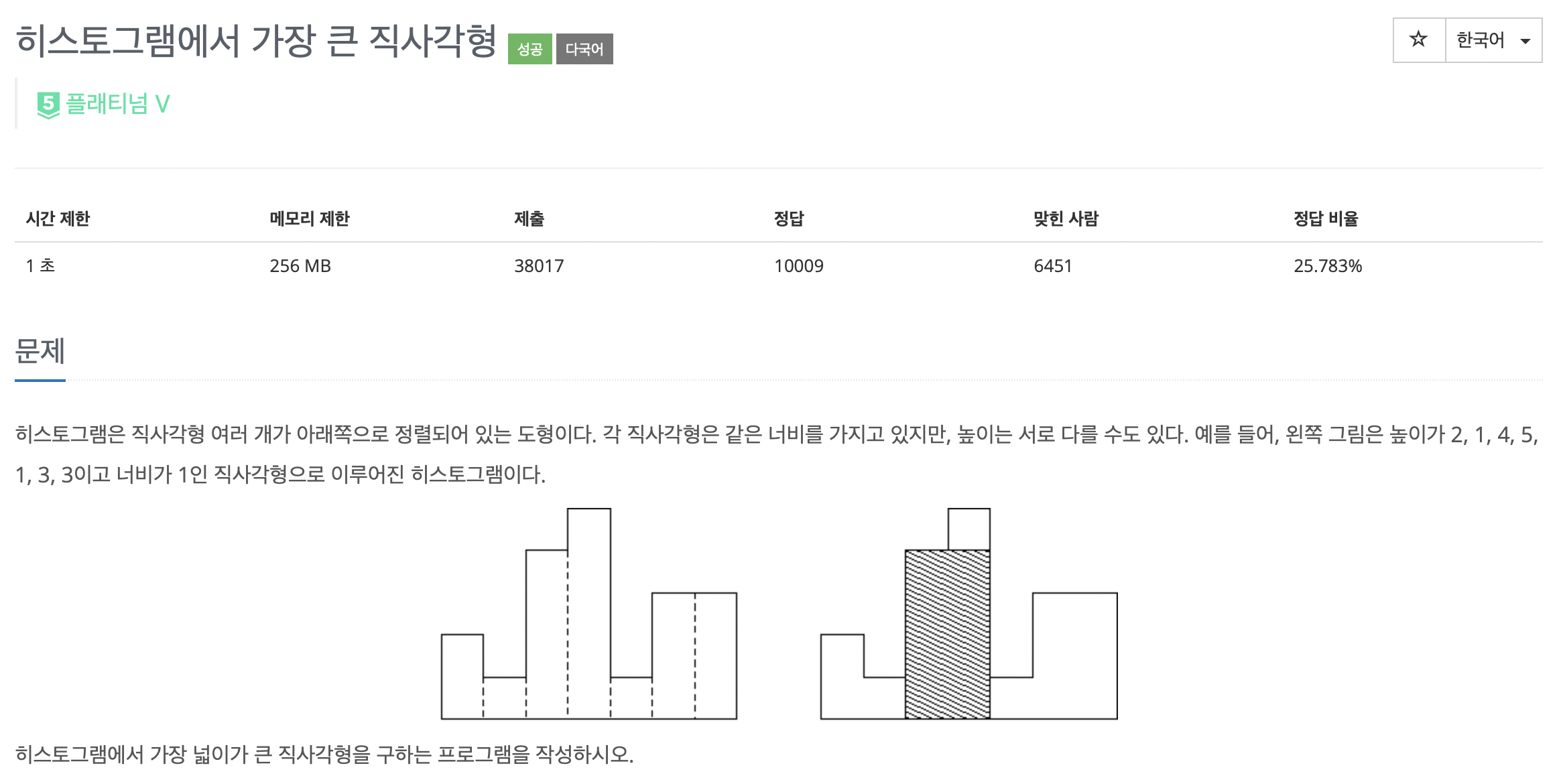
📖 문제
🧑🏻💻 풀이 과정
1) 문제 접근 및 이해
특정 구간의 직사각형 너비를 구하기 위해서는 그 구역의 최소 높이를 알아내야 했습니다.
그리하여 세그먼트 트리를 이용하여 특정 구간의 최소 높이와 최소 높이에 해당하는 숫자의 인덱스 번호를 기록하였습니다.
이후 전체 구간을 시작으로 하여 해당 구역의 직사각형 넓이, 최소 높이의 인덱스를 기준으로 왼쪽과 오른쪽의 직사각형 넓이를 구하였습니다.
분할정복을 이용하여 왼쪽과 오른쪽을 재귀적으로 직사각형의 넓이를 구하며 최대 넓이를 구하였습니다.
2) 알고리즘
- 세그먼트 트리
- 분할정복
3) 풀이 코드
사용 언어 - Python
import sys
sys.setrecursionlimit(100000000)
sys.stdin = open('input.txt')
def make_segement_tree(node, left, right):
if left >= right: # 리프 노드 도달시
segment_tree[node] = (nums[left] , left) # 리프 노드에 각 숫자(높이), 인덱스 기록
return segment_tree[node]
left_tree = make_segement_tree(node*2, left, (left+right)//2) # 왼쪽 자식 노드들의 최소 높이
right_tree = make_segement_tree(node*2+1, (left+right)//2 + 1, right) # 오른쪽 자식 노드들의 최소 높이
if left_tree[0] < right_tree[0]: # 왼쪽 자식들이 더 낮은 높이라면
segment_tree[node] = left_tree # 왼쪽 자식 노드 기록
else:
segment_tree[node] = right_tree # 오른쪽 자식 노드 기록
return segment_tree[node]
def query(node, left, right, start, end): # 구역의 최소 높이와 인덱스 구하기
if end < left or right < start: # 속해있지 않다면 최댓값 반환
return (1e10, -1)
elif start <= left and right <= end: # 완전히 속해있다면, 해당 노드의 값 반환
return segment_tree[node]
left_tree = query(node*2, left, (left+right)//2, start, end)
right_tree = query(node*2+1, (left+right)//2 + 1, right, start, end)
if left_tree[0] < right_tree[0]: # 왼쪽 자식 노드와 오른쪽 자식 노드 비교하여
return left_tree # 더 낮은 높이를 가진 자식 노드 반환
return right_tree
def solution(left, right):
if left >= right: # 너비가 1일 때
return nums[left]
h, idx = query(1, 0, N-1, left, right) # 최소 높이, 그 높이가 해당하는 인덱스
s1, s2, s3 = h * (right-left+1), 0, 0 # 현재 구역의 가능한 넓이
if idx-1 >= left: # 최소 높이의 왼쪽 부분
s2 = solution(left, idx-1)
if idx+1 <= right: # 최소 높이의 오른쪽 부분
s3 = solution(idx+1, right)
return max(s1, s2, s3)
while True:
N, *nums = list(map(int, sys.stdin.readline().split())) # 숫자의 개수, 숫자들
if not N: # 종료
break
segment_tree = {} # 세그먼트 트리 (구역의 최소 높이를 기록)
make_segement_tree(1, 0, N-1) # 세그먼트 트리 생성
print(solution(0, N-1)) # 정답 구하기 및 출력🔗 문제 링크
- https://www.acmicpc.net/problem/6549
6549번: 히스토그램에서 가장 큰 직사각형
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤
www.acmicpc.net
※ 오류 및 오타, 다른 의견이 있는 경우 댓글을 남겨주시면 감사하겠습니다
'알고리즘 문제풀이 > Python' 카테고리의 다른 글
| [백준] 15961 회전 초밥 (0) | 2022.07.16 |
|---|---|
| [백준] 10217 KCM Travel (0) | 2022.07.15 |
| [백준] 14226 이모티콘 (0) | 2022.07.13 |
| [백준] 17135 캐슬 디펜스 (0) | 2022.07.12 |
| [백준] 17143 낚시왕 (0) | 2022.07.11 |




댓글