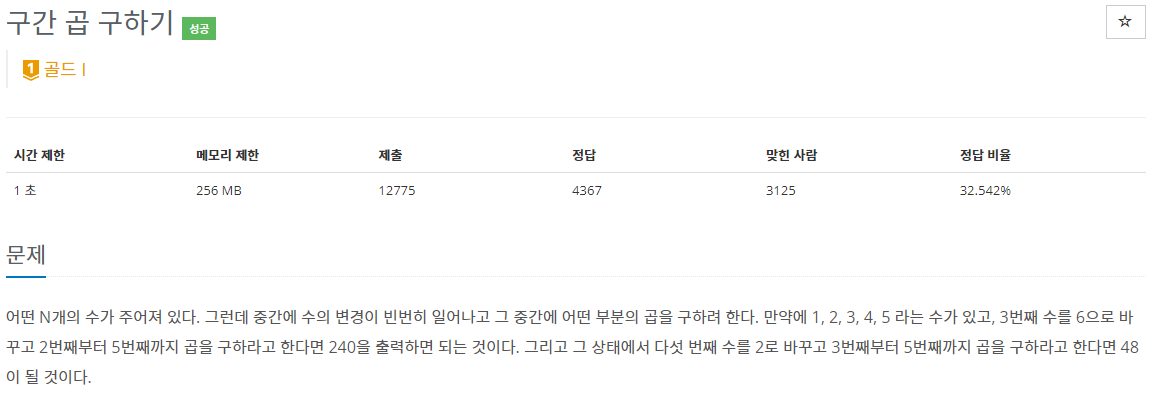
📖 문제
🧑🏻💻 풀이 과정
1) 문제 이해 및 접근
주어지는 입력에 따라 값을 계속해서 변경하고, 변경된 값을 토대로 구간의 곱을 구해야 하므로 세그먼트 트리로 접근했습니다.
2) 알고리즘
- 세그먼트 트리
3) 풀이 코드
사용 언어 - Python
import sys
import math
sys.stdin = open('input.txt')
def init_tree(node, start, end): # 세그먼트 트리 초기화 (현재 노드의 번호, 노드의 범위 시작, 노드의 범위 끝)
if start >= end: # 리프 노드에 도달한 경우
segment_tree[node] = num_li[start] # 리프 노드에 숫자 값 넣기
linked[start-1] = node # 연결관계에 리프노드의 인덱스 추가
return segment_tree[node] # 현재 노드의 값 할당
left = init_tree(node*2, start, (start+end)//2) # 왼쪽 노드들의 곱
right = init_tree(node*2+1, (start+end)//2+1, end) # 오른쪽 노드들의 곱
segment_tree[node] = (left * right) % 1000000007 # 현재 노드의 값을 할당
return segment_tree[node] # 현재 노드 값 반환
def query(node, start, end, left, right): # 쿼리 (현재 노드의 번호, 노드가 가르키는 범위 시작, 범위 끝, 찾으려는 범위의 시작, 끝)
if left <= start and end <= right: # 현재 노드가 찾으려는 범위에 완전히 속할때
return segment_tree[node]
elif left > end or start > right: # 현재 노드가 찾으려는 범위에 완전히 속하지 않을때
return 1
left_nodes = query(node*2, start, (start+end)//2, left, right) # 일부만 겹치면 자식 노드 탐색
right_nodes = query(node*2 + 1, (start+end)//2 + 1, end, left, right)
return (left_nodes * right_nodes) % 1000000007 # 값 반환
def update(node): # 리프 노드의 값 변경에 따른 부모 노드 값 변경
if node <= 0:
return
segment_tree[node] = (segment_tree[node*2] * segment_tree[node*2+1]) % 1000000007
update(node//2)
N, M, K = map(int, sys.stdin.readline().split()) # 수의 개수, 변경 횟수, 구간 곱을 구하는 횟수
num_li = [0] + [int(sys.stdin.readline()) for _ in range(N)] # 숫자 리스트
segment_tree = [0] * 2**(math.ceil(math.log2(N)) + 1) # 세그먼트 트리 생성
linked = [-1] * N # 각 숫자별 저장된 리프 노드의 인덱스
init_tree(1, 1, N)
for _ in range(M+K): # 변경 및 곱 구하는 횟수만큼 반복
a, b, c = map(int, sys.stdin.readline().split()) # 명령의 타입 인덱스, 변경 숫자 / 구하는 구간
if a == 1: # 값 변경의 경우
idx = linked[b-1] # 바꾸려는 값이 위치한 리프노드의 인덱스를 구함
segment_tree[idx] = c # 리프 노드 값 변경
update(idx//2) # 부모 노드들 모두 값 변경
elif a == 2: # 쿼리인 경우
print(query(1, 1, N, b, c)) # 쿼리 조건의 답 구하여 출력📝 결과 및 학습한 내용
1) 어려웠던 내용
세그먼트 관련 내용 중 세그먼트 트리의 적절한 크기 구하기 및 쿼리에 맞는 곱을 탐색하는 과정이 기억나지 않아 어려움을 겪었습니다.
2) 새롭게 학습한 내용
특별히 없습니다.
🔗 문제 링크
- https://www.acmicpc.net/problem/11505
11505번: 구간 곱 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 곱을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
※ 오류 및 오타, 다른 의견이 있는 경우 댓글을 남겨주시면 감사하겠습니다
'알고리즘 문제풀이 > Python' 카테고리의 다른 글
| [백준] 15649 N과 M (1) (0) | 2022.01.14 |
|---|---|
| [백준] 1275 커피숍2 (0) | 2022.01.13 |
| [백준] 14502 연구소 (0) | 2022.01.11 |
| [프로그래머스] 수식 최대화 (0) | 2022.01.10 |
| [프로그래머스] 후보키 (0) | 2022.01.09 |




댓글